みなさん、こんにちは。津新町駅前校の北嶋です。
小学生の皆さん算数は好きですか?
嫌いな人も好きな人もいると思います。
今回は、前回の“難問?珍問?PartⅡ”の解答編になります。
前回の問題難しかったですか?
かなり難しかったと思います。
そんな前回の問題がこちら
直角二等辺三角形ABC中にある水色の台形の面積を求めてみましょう。

それでは、解答を見ていきましょう!! 前回のヒントは“直角二等辺三角形”はいくつあるかな?ですが、みなさんいくつ見つけられました?
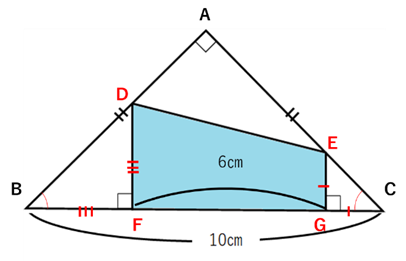
大きな直角二等辺三角形(ABC)と中くらいの直角二等辺三角形(BDF)と小さな直角二等辺三角形(CEG)の3つです。
では、このヒントをもとに解いていきましょう。
一度、図形をこのように動かします。図形問題は動かすと視点がかわりわかりやすくなることがあります。
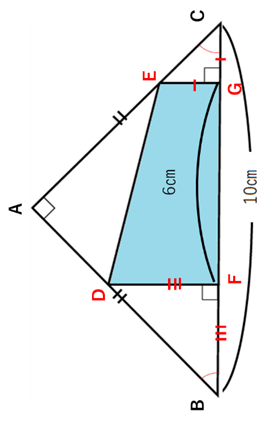
直角二等辺三角形の特徴としては、直角二等辺三角形の文字のごとく1つの角が直角(90°)であり、2つの辺が等しい三角形です。
なので、小さい三角形の辺CGとEGが等しく、中くらいの三角形の辺FBとFDが等しくなります。
ここで台形の面積の公式を思い出してみましょう。
(上底+下底)×高さ÷2
この中で既に長さがわかっているのは高さがわかっています。高さ=6㎝
あとは、上底と下底がわかれば面積が出てきそうです。
三角形①の辺BCの長さは10㎝です。
これは、台形の辺と三角形②と三角形③の辺の合計と等しいです。
なので、10㎝=高さ(6㎝)+CG+FBとなります。
CG=EG(上底)
FB=FD(下底)
なので、FD(上底)+EG(下底)=10㎝-6㎝=4㎝になります。
台形の公式は、(上底+下底)×高さ÷2
なので、上底、下底をそれぞれ求めなくても公式に当てはめることができます。
では、当てはめていきましょう。
4×6÷2=12
よって台形の面積は、12㎠になりました。
また面白い難問、珍問があれば紹介していきます。 さようなら~
【開明 夏期講習ご案内はこちらをクリック↓↓】
